1.本发明属于图像生成技术领域,尤其涉及一种基于变分自动编码器的潜变量空间解耦方法。
背景技术:
2.随着神经网络的不断发展,深度生成已经成为一项创建和操纵数据的强大工具。潜变量空间解耦这一研究方向大多是基于图像或音乐数据集的数据可控性研究。基于潜在表示的模型,例如变分自动编码器(variational auto-encoder)在潜变量空间解耦方面显示出卓越性能。
3.当前大多数无监督解耦方法都是基于vae框架的变化。无监督方法试图解离数据中不同的变化因素,学习其表示形式。此类模型对单个基础变化因子的更改会导致学习到表示形式的单个因子发生更改。例如对潜在空间信息容量施加约束的β-vae模型,最大化潜在编码子集和观测值之间互信息的info-gan模型,以及最大化潜在编码之间独立性潜在变量的β-tcvae模型等。
4.监督方法是通过学习转换关系来控制属性的一类研究。ar-vae模型试图沿着不同维度编码不同的数据属性。midi-vae模型将潜在空间分解为不同的部分,每个部分去对应特定的属性。am-vae模型则是通过学习潜变量空间和属性值之间的转换关系来控制数据属性。以上的监督学习方法也有一些局限性,例如某些方法仅适用于某种类型的数据属性,或者模型需要通过独立改变属性来采样数据点等。
5.以上多数方法能够学习到在每一维度具体的、不相干意义的潜在表示。但其潜在表示的可解释性仍不够强,其可控性和可拓展性较弱。然而在实现潜变量空间解耦的过程中,最重要的是让学习到的表征具备人类可理解的意义,让生成的数据属性更为可控。
技术实现要素:
6.为了弥补现有技术的空白和不足,本发明提出一种基于变分自动编码器的潜变量空间解耦方法,用以实现提高图像潜空间的解耦质量的技术效果。包括编码器模型设计、解码器模型设计、损失函数设计。编码器模型设计阶段使用了自注意力机制和残差网络,使得图像生成模型更有效地捕捉长期依赖关系,增强模型的维度适应性;解码器模型设计阶段将潜变量空间编码z解码,实现图像重构;损失函数设计阶段使得潜变量空间编码维度与属性值趋向单调关系,从而达到优化训练的目的。通过设计良好的编解码模型和损失函数,实现对图像数据的特征映射和参数调整,实现有效的数据降维,并保留高度的图像特征。在确保图像重建精度的前提下让解耦的潜变量空间具备更好的可解释性和模块化特征,提高潜变量空间解耦性能。
7.本发明具体采用以下技术方案:
8.一种基于变分自动编码器的潜变量空间解耦方法,其特征在于:基于图像编解码模型和训练阶段损失函数;所述编解码模型包括以自注意力机制和残差网络构建的编码器
和使用线性层和转置卷积层的解码器;所述损失函数包括vae重构损失、kld散度损失和潜变量空间解耦损失,包括以下步骤:
9.步骤s1:根据图像生成模型建立训练集,使每张数字图片拥有使用形态测量学获得的属性;
10.步骤s2:将步骤s1获得的训练集图像输入编码器网络,得到三种矩阵q、 k、v以用作自注意力机制模型的输入;
11.步骤s3:将步骤s2获得的三种矩阵进行自注意力机制下的运算,得到自注意力机制模型的输出w-v矩阵;
12.步骤s4:将步骤s3获得的w-v矩阵与输入图像相加构成残差链接,再通过线性层输出为模型所需的潜变量空间编码z;
13.步骤s5:将步骤s4获得的潜变量空间编码z传入解码器,实现图像的重构;
14.步骤s6:通过损失函数确保所述潜变量空间解耦维度与属性值呈单调关系。
15.进一步地,步骤s1建立训练集操作具体包括以下步骤:
16.步骤s11:将图片放大;
17.步骤s12:二值化处理:将模糊的放大图像在其强度范围的一半进行阈值处理,以确保不会删除细小的或模糊的数字;
18.步骤s13:计算欧氏距离变换edt:数字边界内的每个像素都包含到其最近边界点的距离;
19.步骤s14:提取骨架:检测edt处理后的纹路,即检测与两个或多个边界点等距的点的轨迹;
20.步骤s15:运用提取出来的骨架信息为每个数字计算多种形态测量属性;
21.步骤s16:将图像缩小到原始分辨率。
22.进一步地,在步骤s16之前,对二值化图像应用扰动;之后将扰动的图像缩小到原始分辨率。
23.进一步地,在步骤s1中,选取2-d sprites、morpho-mnist数据集总体的70%作为训练集,20%作为验证集,10%作为测试集。
24.进一步地,在步骤s2中,通过线性层将学到的数据分布式特征表示映射到样本标记空间,得到查询矩阵q(query)、键矩阵k(key)和值矩阵v(value);并将q和k网络的输出矩阵相乘,计算两者相关性,得到q-k矩阵: similarity(q,ki)=q
·ki
。
25.进一步地,在步骤s3中,首先使用softmax激活函数得到w,对原始分值进行归一化处理,将q和k的缩放点积转化为注意力的相对测量,计算结果ai即为v对应的权重系数,即:接下来根据权重系数对v 进行加权求和,将softmax激活后的w与v矩阵相乘,得到:最后将得到的w-v矩阵和输入图像x进行元素级相乘,得到自注意力机制的输出w-v;总的自注意力机制为:
26.进一步地,在步骤s4中,在得到qkv网络的输出后,将这一部分输出与输入图像相
加,构成残差连接传到线性层,并从线性层输出模型所需的潜变量空间编码z。运用残差网络把输入图像直接映射到后面的网络层中,确保后面的网络层一定比前面包含更多的图像信息。这样能够避免网络退化现象,也能够避免可能存在的梯度消失问题。
27.进一步地,在步骤s5中,使用三层线性层和四层转置卷积层将潜变量空间编码z解码,实现图像的重构;每一个线性层和卷积层后都选择使用relu函数进行激活。relu函数在一定程度上增加了网络模型的稀疏性,使得模型提取出来的特征更具代表性。在相对小的运算量区间内成功提高网络的泛化性能。
28.进一步地,在步骤s6中,所述损失函数损失函数损失由三部分构成,分别是vae重构损失、kld散度损失和潜变量空间解耦损失。表达式为:
[0029][0030]
其中:β》1,鼓励潜在空间维度的独立性;γ为可调超参数,代表正则化强度;l为属性个数,
[0031]
本发明及其优选方案编码器模型设计阶段使用了自注意力机制和残差网络,使得图像生成模型更有效地捕捉长期依赖关系,增强模型的维度适应性;解码器模型设计阶段将潜变量空间编码z解码,实现图像重构;损失函数设计阶段使得潜变量空间编码维度与属性值趋向单调关系,从而达到优化训练的目的。通过设计良好的编解码模型和损失函数,实现对图像数据的特征映射和参数调整,实现有效的数据降维,并保留高度的图像特征。在确保图像重建精度的前提下让解耦的潜变量空间具备更好的可解释性和模块化特征,提高潜变量空间解耦性能。
附图说明
[0032]
图1为本发明实施例提供的一种用于潜变量空间解耦的编码器模型示意图。
[0033]
图2为本发明实施例提供的一种用于潜变量空间解耦的解码器模型示意图。
[0034]
图3为本发明实施例提供的三种不同方法下的可解释性解耦指标分数示意图。
[0035]
图4为本发明实施例提供的三种不同方法下的模块化解耦指标分数示意图。
[0036]
图5为本发明实施例提供的三种不同方法下的互信息间隔解耦指标分数示意图。
[0037]
图6为本发明实施例提供的三种不同方法下的分离属性可预测性解耦指标分数示意图。
[0038]
图7为本发明实施例提供的三种不同方法下的斯皮曼相关系数得分解耦指标分数示意图。
[0039]
图8为本发明实施例提供的2-d sprites属性遍历图像示意图。
[0040]
图9为本发明实施例提供的morpho-mnist属性遍历图像示意图。
[0041]
图10为本发明实施例提供的三种不同方法下的重构准确率对比示意图。
具体实施方式
[0042]
为让本专利的特征和优点能更明显易懂,下文特举实施例,作详细说明如下:
[0043]
应该指出,以下详细说明都是例示性的,旨在对本技术提供进一步的说明。除非另有指明,本文使用的所有技术和科学术语具有与本技术所属技术领域的普通技术人员通常理解的相同含义。
[0044]
需要注意的是,这里所使用的术语仅是为了描述具体实施方式,而非意图限制根据本技术的示例性实施方式。如在这里所使用的,除非上下文另外明确指出,否则单数形式也意图包括复数形式,此外,还应当理解的是,当在本说明书中使用术语“包含”和/或“包括”时,其指明存在特征、步骤、操作、器件、组件和/或它们的组合。
[0045]
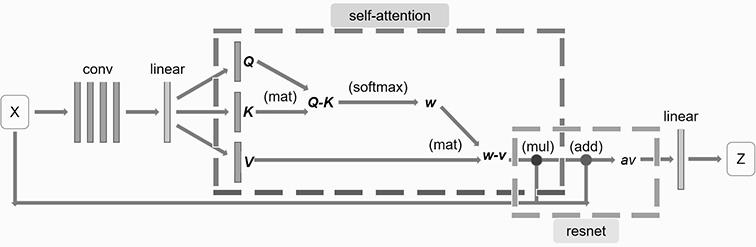
参见图1,图1为本发明实施例提供的一种用于潜变量空间解耦的编码器模型示意图。
[0046]
本编码器结构模型如图1所示。在编码器上,运用了四层卷积层和一层线性层对图像数据进行特征映射和参数调整,能够有效地实现数据降维,并且高度保留图像特征。随后将处理后的数据传入自注意力机制模型,捕捉数据特征的内部相关性。
[0047]
参见图2,图2为本发明实施例提供的一种用于潜变量空间解耦的解码器模型示意图。
[0048]
本解码器结构模型如图2所示。在解码器阶段,使用三层线性层和四层转置卷积层将潜变量空间编码z解码,实现图像的重构。在每一个线性层和卷积层后都选择使用relu函数进行激活。relu函数在一定程度上增加了网络模型的稀疏性,使得模型提取出来的特征更具代表性。在相对小的运算量区间内成功提高网络的泛化性能。值得一提的是,在编码器和解码器阶段因参数量更少,较ar-vae 而言实现了更为轻量级的模型架构。
[0049]
参见图3,图3为本发明实施例提供的三种不同方法下的可解释性解耦指标分数。
[0050]
ta-vae将可解释性(interpretability)指标从0.85提升到了0.91。这说明ta-vae 使用潜在空间的某一个维度预测给定数据属性的能力较ar-vae更优。可解释性指标是潜变量空间解耦任务中最关键的指标。在可解释性上的大幅提升证明了 ta-vae模型优越的潜变量空间解耦能力。
[0051]
参见图4,图4为本发明实施例提供的三种不同方法下的模块化解耦指标分数。
[0052]
模块化度量(modularity)指标上ta-vae与ar-vae持平。这可以通过观察所使用的指标计算方法进行解释。其计算过程中分数除以具有潜在维度的所有属性的互信息的最大值θi。这样就导致即使ar-vae模型互信息的值相对较低,却也能够得到较高的模块化得分。
[0053]
参见图5,图5为本发明实施例提供的三种不同方法下的互信息间隔解耦指标分数。
[0054]
互信息间隔(mig)指标略低于ar-vae。这表明潜变量空间中除了解耦属性的维度之外,还有其他维度与不同属性共享高度的互信息。
[0055]
参见图6,图6为本发明实施例提供的三种不同方法下的分离属性可预测性解耦指标分数。
[0056]
分离属性可预测性(sap)从0.85提升到0.91。这说明ta-vae模型中每个潜变量空间维度更依赖于某一个属性值,属性在潜变量空间编码的分离效果上较 ar-vae更优。
[0057]
参见图7,图7为本发明实施例提供的三种不同方法下的斯皮曼相关系数得分解耦指标分数。
[0058]
斯皮曼相关系数得分(scc)从0.88提升到了0.95。这样的跃升说明ta-vae模型某
一属性的属性值与潜变量空间编码维度之间具有更为良好的单调关系。
[0059]
参见图8,图8为本发明实施例提供的2-d sprites属性遍历图像。
[0060]
2-d sprites数据集中有三种形状类别(正方形、心形和椭圆形)。图8分别是三个模型在数据集上的属性遍历重构图像。这里展示心形图像进行对比。每一组图像内的不同列对应了沿着潜在空间维度对某种特定属性进行编码,从左到右的五列分别遍历了形状、大小、方向、x轴位置、y轴位置这五种属性。
[0061]
观察重构图像可以发现β-vae重构效果最差。大小属性遍历的最后一个图像以及在心形旋转时都无法准确还原出心形。这说明β-vae的潜变量空间解耦程度最低,难以实现很好的属性遍历效果。ar-vae和ta-vae在重构图像上明显更优。但ar-vae在x轴遍历的最后一个图像上生成心形较ta-vae更为模糊。
[0062]
参见图9,图9为本发明实施例提供的morpho-mnist属性遍历图像。
[0063]
morpho-mnist数据集中共有0到9十种数字。图9分别列出三个模型在数据集上的属性遍历重构。这里展示数字7图像进行对比。每一组图像内的不同列对应了沿着潜在空间维度对某种特定属性进行编码,从左到右的六列分别是面积、长度、厚度、斜度、宽度、高度的遍历。
[0064]
观察重构图像可以发现morpho-mnist数据集上三个模型的表现都不如2-dsprites数据集。β-vae的重构图像最差,生成图像十分模糊。ar-vae和ta-vae 在重构图像的清晰度以及属性遍历的完整度上明显更优。沿着潜变量空间的特定维度进行遍历,手写体数字的各种属性都在不断变大。但是在长度属性遍历中的最后一个图像上ta-vae的长度较ar-vae明显更长,厚度属性中ta-vae的重构图像也更为清晰,厚度更大。
[0065]
参见图10,图10为本发明实施例提供的三种不同方法下的重构准确率对比。
[0066]
重构准确率是评估生成模型的重要指标。本实验测量了三种不同模型对2-dsprites图像以及morpho-mnist手写体数据集的重构准确率,如图10所示。三个模型在2-d sprites数据集的重构准确率都很高。β-vae为99.65%,ar-vae和 ta-vae都高达99.90%。在morpho-mnist数据集,β-vae为94.20%,ar-vae为 97.10%,ta-vae为97.20%。虽然于目前的解耦任务而言重构准确率相对较高,并且提高解耦能力可能要以牺牲重构为代价。但本文模型在解耦性能更好的情况下,重构准确率仍远高于β-vae,并且高于ar-vae。这也证明了本模型在潜变量空间解耦上的良好性能。
[0067]
本专利不局限于上述最佳实施方式,任何人在本专利的启示下都可以得出其它各种形式的基于变分自动编码器的潜变量空间解耦方法,凡依本发明申请专利范围所做的均等变化与修饰,皆应属本专利的涵盖范围。
基于变分自动编码器的潜变量空间解耦方法相关文章:
★ 变分自编码器解析